残剑

Stop walking today and you'll have to run tomorrow!

链栈

| Comments

栈是限制在表的一端进行插入和删除运算的线性表。通常称插入、删除的这一端为栈顶，另一端称为栈底；当表中没有元素时称为空栈；栈为后进先出的线性表，简称为LIFO表；栈的修改是按后进先出的原则进行；每次删除的总是当前栈中最新的元素（即最后插入的元素），而最先插入的被放在栈的底部，要到最后才能删除。

链栈结点

出栈与入栈是栈的最主要操作，当无法预见栈所需大小时，往往需要采用链栈的方式。在链栈中，不需要像单链表一样需要头结点。链栈的结构如下图所示：

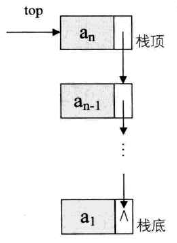
stacknode

可将其结构定义为：

1
2
3
4
5
6
7
8
9
10
11
12
13

typedef char SElemType

typedef struct StackNode
{
    SElemType data;//根据实际需要定义数据类型
    struct StackNode *next;
}StackNode,*LinkStackPtr;

typedef struct LinkStack
{
    LinkStackPtr top;//指向栈链顶部
    int count;//用以判断栈是否为空，可初始化为0
}LinkStack;

进栈

能够进栈的前提是已成功建立栈空间。进栈函数所需的参数主要是指向栈顶的指针和入栈的内容，因此可定义为：

1

int Push(LinkStack *pS, SElemType e);

进栈操作的过程如下图所示:

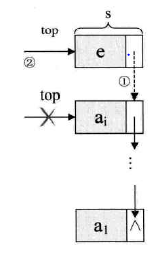
stackpush

Step1：开辟内存，将需要入栈的元素压入栈；

1
2

LinkStackPtr s = (LinkStackPtr)malloc(sizeof(StackNode));
s->data = e;

Step2：更改指针；

1
2

s->next = pS->top; //新结点的next指向原来栈顶
pS->top = s; //链栈新的top指针指向新建立的结点

Step3：更改栈状态（累计入栈元素个数）。

1

pS->count++;

出栈

出栈之前需要判断当前栈的状态，如果栈元素个数为零，则是空栈，无法进行出栈操作。出栈操作函数同样需要两个参数，一是指向链栈的指针，二是弹出的栈元素，因此定义为：

1

int Pop(LinkStackPtr *pS, SElemType *e); //之所以是*e，是为了在函数结束后可以取得该弹出元素

出栈操作过程如下图所示：

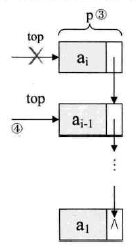
stackpop

Step1：获取弹出元素；

1

*e = pS->top->data;

Step2：top指针指向栈顶；

1
2

p = pS->top ;
pS->top = p->next;//LinkStackPtr p;

Step3：释放结点；

1

free(p);

Step4：更改栈状态。

1

pS->count--;

测试程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106

#include <stdlib.h>
#include <string.h>
#include <stdio.h>

typedef char SElemType;

typedef struct StackNode {
    SElemType data;
    struct StackNode *next;
} StackNode, *LinkStackPtr;

typedef struct LinkStack {
    LinkStackPtr top;
    int count;
} LinkStack;

void InitialStack(LinkStack * L)
{
    L->top = NULL;
    L->count = 0;
    
    return;
}

int StackEmpty(LinkStack * pS)
{
    return (!pS->count);
}

int Push(LinkStack * pS, SElemType e)
{
    LinkStackPtr s = (LinkStackPtr) malloc(sizeof(StackNode));
    if(s == NULL) {
        printf("no enough memory!\n");
        return -1;
    }
    s->data = e;
    s->next = pS->top;
    pS->top = s;
    pS->count++;
    
    return 0;
}

int Pop(LinkStack * pS, SElemType * e)
{
    LinkStackPtr p = NULL;
    
    if (StackEmpty(pS)) {
        printf("stack is empty！\n");
        return 0;
    }

    *e = pS->top->data;
    p = pS->top;
    pS->top = p->next;
    free(p);
    pS->count--;
    
    return 0;
}

void PrintStackLink(LinkStack * pS)
{
    int i;
    LinkStackPtr L = NULL;
    
    L = pS->top;
    if (StackEmpty(pS)) {
        printf("stack is empty！\n");
        return;
    }

    for (i = 0; i < (pS->count); i++) {
        printf("%c\n", L->data);
        L = L->next;
    }
    
    return;
}

int main(int argc, char **argv)
{
    char getch;
    char outch;
    LinkStack myStack;
    
    InitialStack(&myStack);
    
    printf("请输入压入栈的数据（char型），输入#结束:\n");
    scanf("%c", &getch);
    while (getch != '#') {
        Push(&myStack, getch);
        scanf("%c", &getch);
    }
    printf("栈链内容为：\n");
    PrintStackLink(&myStack);

    while (!StackEmpty(&myStack)) {
        Pop(&myStack, &outch);
        printf("弹出内容为：%c\n", outch);
    }
    PrintStackLink(&myStack);

    return 0;
}

Comments